3. F.E. model of the arch
After the preliminary analysis described above, more
accurate structural analyses have been performed, starting with the
creation of a F.E. model of the arch with the well-known computer-code
SAP2000. The obtained results were compared with the ones of the
preliminary analysis to check their reliability.
The SAP2000 code allows only for linear elastic
calculations of the structures, and consider a material with infinite
strengths both in compression and in tension. Therefore, at the end of the
analyses, it has been checked that the sections were not partialised.
The arch model consists of "beam" elements
that lie along the axis line of the actual arch (this condition is
important to attain a reliable evaluation of the funicular polygon).
In the F.E. model the dead loads of the following
elements have been applied:
- arch
- spandrels
- stiffening rib
- stone slabs that connect horizontally the stiffening rib and the
spandrels
- filling material and threading surface
- parapets
The mechanical characteristics of the material,
calculated as approximate values, are:
E= 100000 Kg / cm2 and n
=0.15.
The trend of the stress resultants attained are
illustrated here at the sketch:

fig. 3 - Undeformed
configuration
fig. 4 - Deformed
Configuration
fig. 5 - Normal forces
fig. 6 - Bending moments.
In order to evaluate the reliability of the model, we
have calculated the trend of the thrust line by dividing the bending
moment by the normal force at each section.
The trend of the curve of thrusts is represented
(figure 07) in red, the arch is identified by means of continuous black
lines, the envelope of the third medium lines by dotted black lines.
Finally, the axis is identified by means of a black hatched and dotted
line.
It is useful to observe that the trend of the curve is
limited within the third medium line. The axial thrust value is out of
tolerance only in the area that corresponds to the central inertia core of
the areas shown. The keystone section is the one that suffers the higher
traction stress, with an eccentricity of the load from the axis line of
22.2 cm, that can be calculated with the following formula:
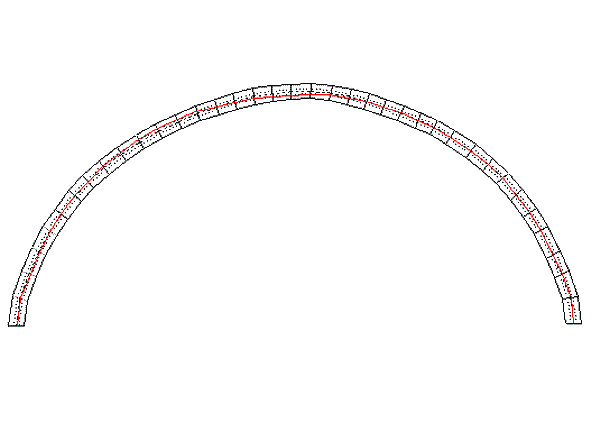
fig. 7 - Thrust line
s t = 2 N / (3 u
b) = 19.93 kg/cm2,
where
- N is the axial thrust equivalent to N = 191945 kg,
- Mf is the bending thrust equivalent to Mf =
4287994 kgcm,
- b is the base of the section equivalent to b = 400 cm,
- u is the distance of N from the edge equivalent to h = 16.05 cm.
- If we assume the section to be not partialised, then the stresses
are:
- s t = N / (b h) + (6 Mf)
/ (b h2) = 4.7 kg/cm2 (both in compression and
in tension)
that is the stresses are higher than the traction limit
of the masonry.
As in the past the former bridge did not exhibit
stability problems and diffused cracking patterns, these stresses could
not be present in the arch, which means that the actual bearing structure
was formed by the arch and the overlying spandrels and slab.
Moreover, these results highlight the deviation of the
funicular polygon on the left side from the arch axis as opposed to the
opposite arcade. The above considerations are confirmed by the stretching
of the curved axis of the left arch.
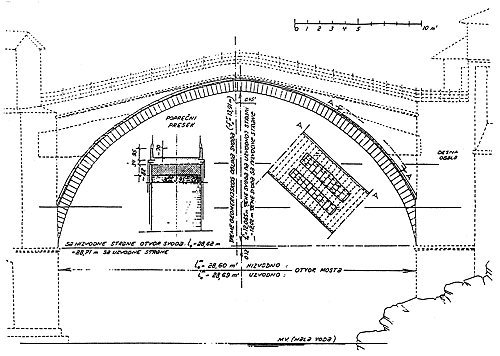
fig. 8 - Section of arch.
Notice the collapse of the abutment
On the basis of the above results, a refined F.E. model was created.
|